Planning units.
Planning units are the building blocks of any conservation or zoning plan. They convert the world into smaller more manageable pieces that can be treated separately from one another, similar to a jigsaw puzzle. Each planning unit contains information about their corresponding location on Earth.


Each planning unit has a unique identification number, this number with the biological or socio-economic information attached is what feeds into conservation planning softwares (such as Marxan).
PLANNING UNIT SIZE AND SHAPE.
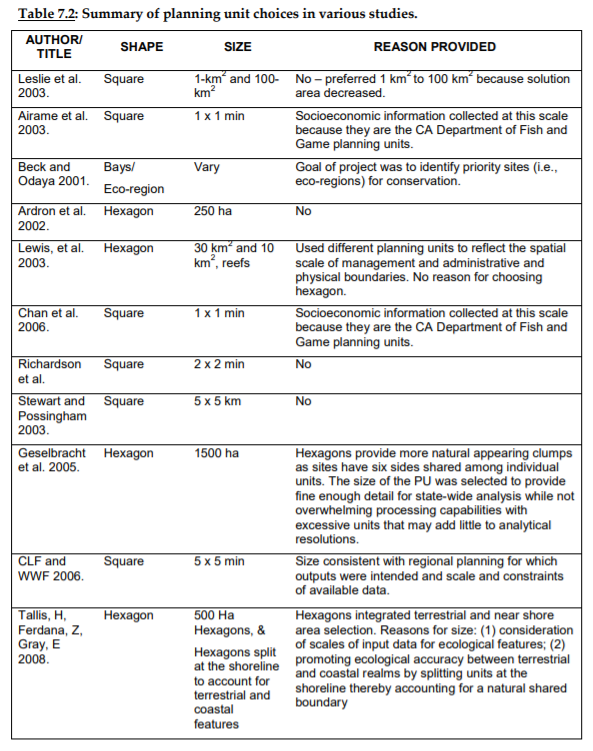
There are many considerations that should go into determining the appropriate size and shape of planning units. There isn’t a one‐size fits all solution, and the appropriate size and shape will depend on the circumstances of each individual planning exercise. In general, planning unit size and shape is informed by a combination of: the scale of planning (i.e., global, regional, national or local); the resolution of datasets being used; the objective of planning exercise and the intended use of the outputs (e.g., general area prioritisation or specific plans for implementation such as a comprehensive zoning scheme).
NUMBER OF PLANNING UNITS.
What is the maximum number of planning units that Marxan can process? Technically, there was an upper limit of around 20 000 to 30 000 on the number of planning units that early versions of Marxan could handle (version 1.8.10 and earlier), though the optimised version (version 2.0+) has less restrictions and has been successful at processing much larger numbers, over 100 000, or even 150 000 planning units on newer computers with ample RAM memory. However, computer horsepower aside, there are mathematical reasons why Marxan, with its algorithms that try to do a reasonable job with optimality, will struggle to successfully process large numbers of PUs and features into an efficient, and hence meaningful, solution.
The number of possible network solutions is 2 to the power of the number of PUs. Thus, 100 000 PUs is more than 10 to the power 10 000 possible solutions which is greater than number of atoms in universe! That said, there are some cases where the decision space is so constrained by the arrangement of its features that even with huge numbers of PUs, near‐optimal results are still tractable. However, these situations are the exception, and in general, when there are lots of possible network configurations, optimal solutions will be hard to find when using over 50 000 PUs.
Considering issues of scale and precision, blocking fine‐scale raster data into sub‐catchments and hexagons really does not cause you to lose any data and it should not be seen as a problem. Ultimately, it is all about the spatial scale of decision‐making. If decision‐making in a large study area is still on the scale of individual hectares then the problem has to be divided into sub‐regional analyses. However, usually this is not thecase. If required, sequential or greedy algorithms can work on such huge numbers of PUs but it is very unlikely that the solutions produced would be anywhere near optimal.
Thus, good practice would dictate either aggregating data into larger PUs or sub‐dividing the study area. If you do decide to use a large number of PUs, you will need to do extensive testing to find the number of iterations required whereby the good solutions begin to converge. Even with the latest desktop computers, getting meaningful near‐optimal solutions could increase processing time dramatically, perhaps 24 hours or longer per Marxan scenario.
FOR MORE INFORMATION.
Ardron, J.A., Possingham, H.P., and Klein, C.J. (eds). 2010. Marxan Good Practices Handbook, Version 2. Pacific Marine Analysis and Research Association, Victoria, BC, Canada. 165 pages. https://pacmara.org/wp-content/uploads/2010/07/Marxan-Good-Practices-Handbook-v2-2010.pdf
